17. Hyperparameters
Hyperparameters for Decision Trees
In order to create decision trees that will generalize to new problems well, we can tune a number of different aspects about the trees. We call the different aspects of a decision tree "hyperparameters". These are some of the most important hyperparameters used in decision trees:
Maximum Depth
The maximum depth of a decision tree is simply the largest possible length between the root to a leaf. A tree of maximum length
k
can have at most
2^k
leaves.
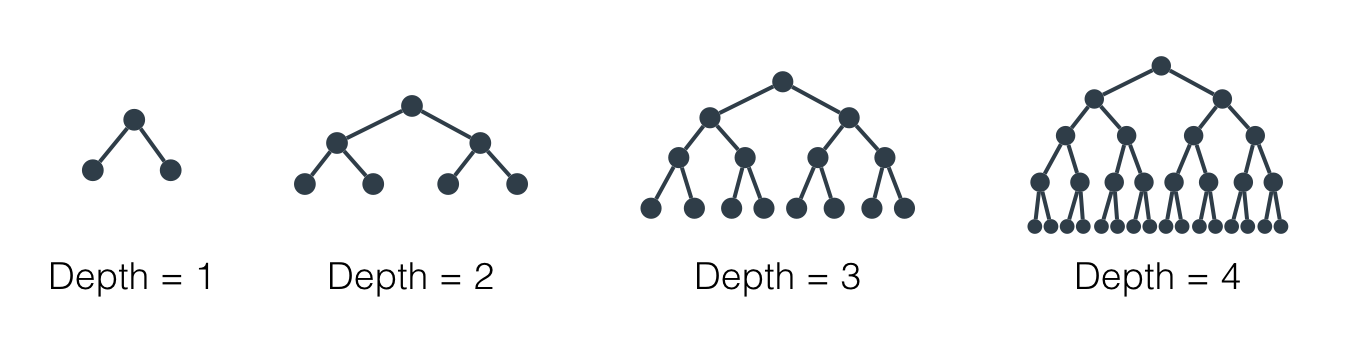
Maximum depth of a decision tree
Minimum number of samples to split
A node must have at least min_samples_split samples in order to be large enough to split. If a node has fewer samples than min_samples_split samples, it will not be split, and the splitting process stops.
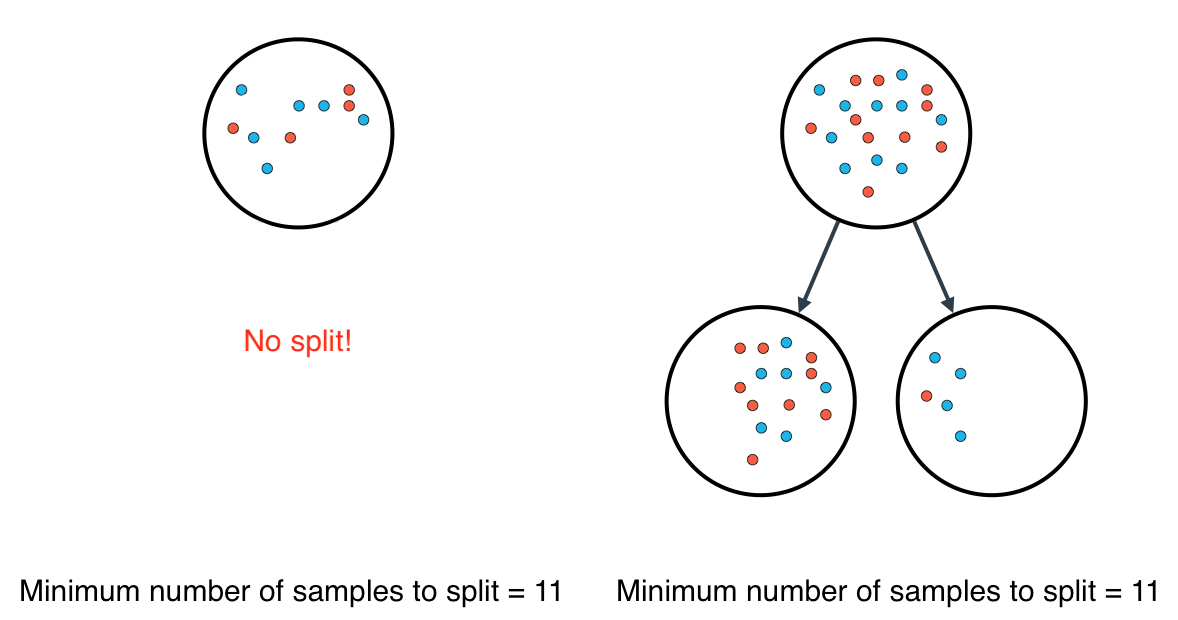
Minimum number of samples to split
However, min_samples_split doesn't control the minimum size of leaves. As you can see in the example on the right, above, the parent node had 20 samples, greater than min_samples_split = 11, so the node was split. But when the node was split, a child node was created with that had 5 samples, less than min_samples_split = 11.
Minimum number of samples per leaf
When splitting a node, one could run into the problem of having 99 samples in one of them, and 1 on the other. This will not take us too far in our process, and would be a waste of resources and time. If we want to avoid this, we can set a minimum for the number of samples we allow on each leaf.

Minimum number of samples per leaf
This number can be specified as an integer or as a float. If it's an integer, it's the minimum number of samples allowed in a leaf. If it's a float, it's the minimum percentage of samples allowed in a leaf. For example, 0.1, or 10%, implies that a particular split will not be allowed if one of the leaves that results contains less than 10% of the samples in the dataset.
If a threshold on a feature results in a leaf that has fewer samples than min_samples_leaf, the algorithm will not allow that split, but it may perform a split on the same feature at a different threshold, that does satisfy min_samples_leaf.
Overfitting Underfitting quiz
QUIZ QUESTION::
Let's test your intuition. Which sizes of features are associated with underfitting and which with overfitting? Drag the answers to the corresponding boxes.
ANSWER CHOICES:
|
Feature |
Underfitting/Overfitting |
|---|---|
Small maximum depth |
|
Large maximum depth |
|
Small minimum samples per split |
|
Large minimum samples per split |
SOLUTION:
|
Feature |
Underfitting/Overfitting |
|---|---|
|
Small maximum depth |
|
|
Large minimum samples per split |
|
|
Large maximum depth |
|
|
Small minimum samples per split |
|
|
Large maximum depth |
|
|
Small minimum samples per split |
|
|
Small maximum depth |
|
|
Large minimum samples per split |